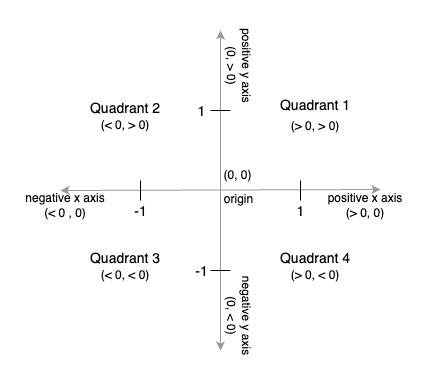
- quadrant 1: x > 0, y > 0
- quadrant 2: x < 0, y > 0
- quadrant 3: x < 0, y < 0
- quadrant 4: x > 0, y < 0
- origin: x = 0, y = 0
- positive x-axis: x > 0; y = 0
- negative x-axis: x < 0; y = 0
- positive y-axis: x = 0; y > 0
- negative y-axis: x = 0; y < 0
Prep
I've provided some simpler preliminary Codelab exercises that contain some of the coding you need to do:- printing a point
- creating a
Scannervariable - reading in points from a file
- calculating the region of a point
Points
As mentioned above, a point is a unique location in the plane. It is said to be in that it has no height or width (and thus no length). A point is represented as a pair in the form (x, y) where x and y are the positions on the x and y axes respectively opposite the point: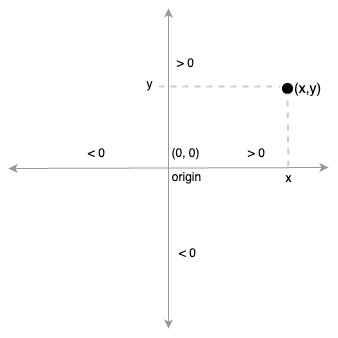 For the purposes of this assignment we will restrict ourselves to integer-valued points (e.g., (0, 1) and (5, -7) as opposed to real points such as (3.1, -.2.45)).
For the purposes of this assignment we will restrict ourselves to integer-valued points (e.g., (0, 1) and (5, -7) as opposed to real points such as (3.1, -.2.45)).
Lab 0.1
Write a full Java app that reads in points from a file and prints them out together with their region. You should have the following methods:- int getRegion(int x, int y): — return which region the point lies in/on. This returns an integer value between 0 and 8: 0 being the origin, 1-4 being the corresponding quadrant, and 5-8 being the positive x-axis, negative x-axis, positive y-axis, negative y-axis respectively.
- print(int x, int y) : prints the point in the format (x, y) to System.out
Lines
Lineas are represented by their two endpoints (strictly speaking, these are line segments, lines are infinite, but we'll stick with this terminology for this lab).Length
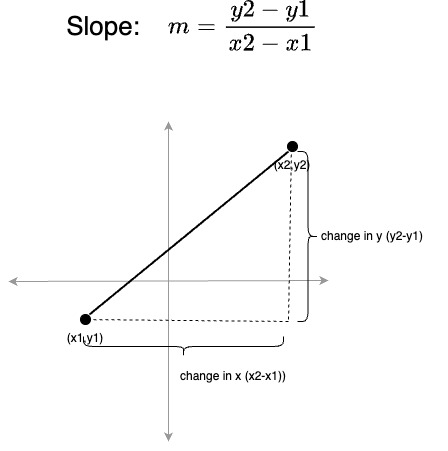
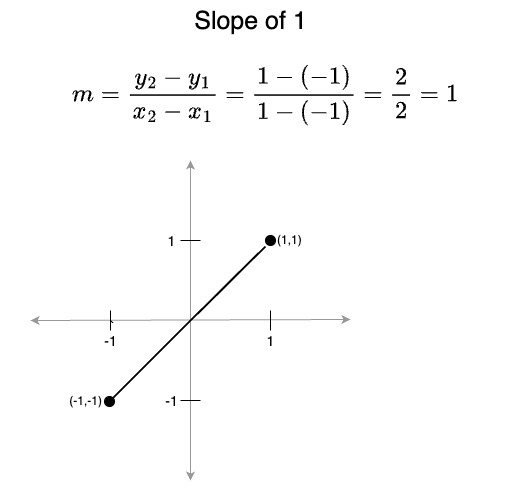
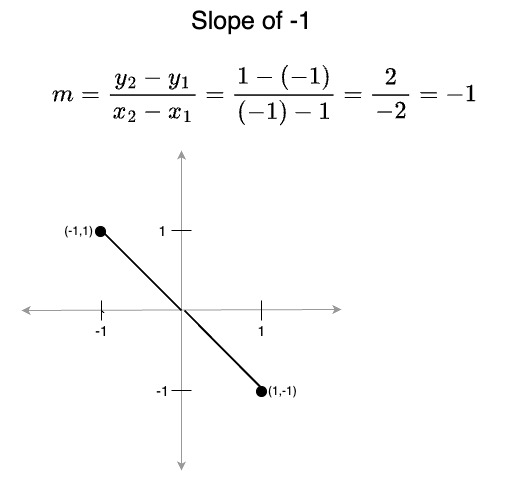
A line has length or distance. Using the Pythagorean theorem, we see that the length between the two endpoints (the line itself, which is the hypotenuse of the right triangle) is the square root of the sum of the squares of the two sides (the x and y components). A line has the notion of a slope which is the amount of change in y relative to a change in x. Slope is calculated by taking the ratio of the change in y between two points relative to the change in x for those same points: (Slope is usually represented by the letterm for various reasons).
Here are some properties of the slope of a line:
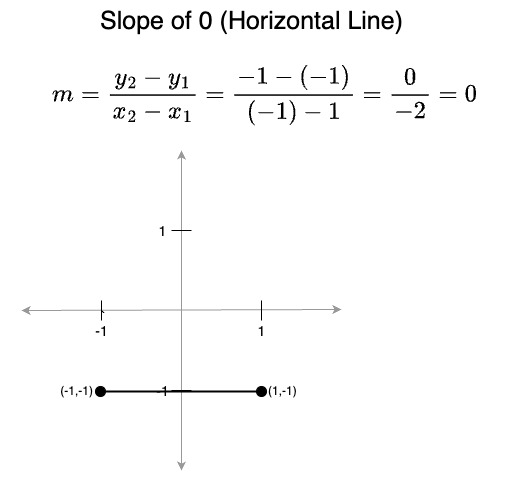
- A slope of 0 means that y doesn't change, i.e., the line is horizontal (parallel to the x axis):
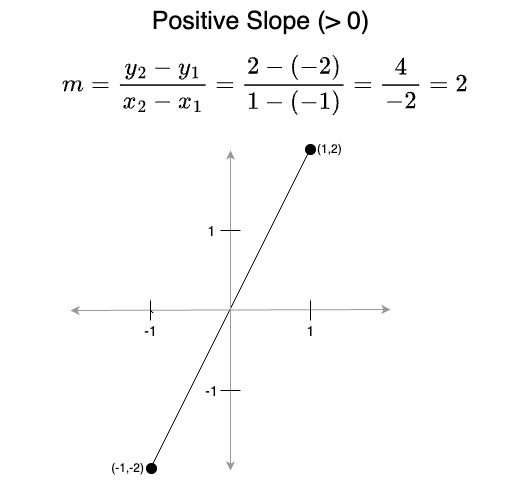
- A slope greater than 0 represents a line the is moving upwards from left to right
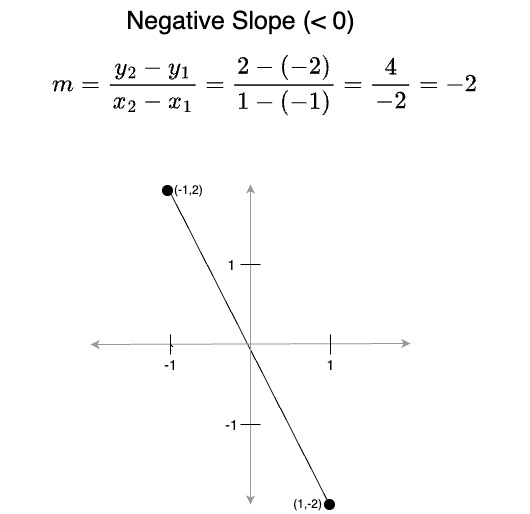
- A slope less than 0 represents a line that is moving downwards from left to right
- A slope of 1 means x and y change at the same rate; i.e., the line rises at a 45° angle from left-to-right
- A slope of -1 means x and y change at the same rate, but here the line descends at a 45° angle from left-to-right
- A vertical line has no slope - the x value is not moving, and thus the y component increases 'infinitely' with respect to x
- In terms of the slope equation, the denominator is 0 (since both x values are the same) which would result in a division-by-zero, thus the slope is undefined
- A slope between 0 and 1 (or between 0 and -1) is shallow, the line makes more horizontal progress than vertical progress
- A slope greater than 1 (or less than -1) is steep, the line makes more vertical progress than horizontal progress
Line Pairs
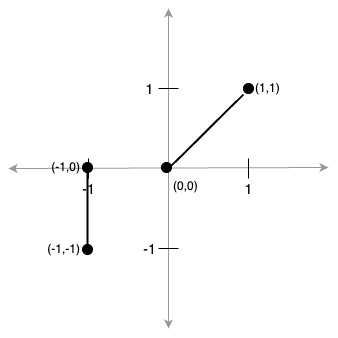
Our last investigation of the Cartesian plane will be pairs of lines. These are simply represented as two lines, each line represented — as above — using two endpoints; e.,g (0, 0), (1, 1) and (-1, -1), (-1, 0):Parallel, and Perpendicular
- Two lines are parallel if they have the same slope
- If they both rise at the same rate they will never intersect
- On the other hand if the slopes of the two lines are negative reciprocals of each other
(i.e., one has slope
mand the other-1/m, then the lines are perpendicular to each other.
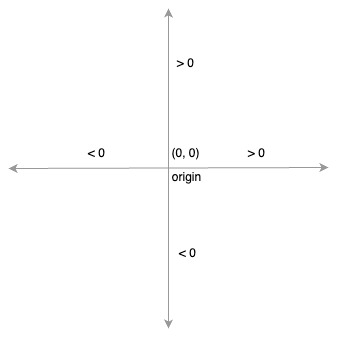 The plane is thus divided into nine regions: the origin, four
The plane is thus divided into nine regions: the origin, four