CISC 3115 — Lab #1

CISC 1115
Introduction to Modern Programming Techniques
An Overview of Points, Lines, Line Pairs

The Plane

The Cartesian Plane is a two dimensional representation used for mapping points, lines, shapes, mathematical functions, etc. It is usually displayed as a perpendicular pair of lines, known as the x and y axes, which cross at a unique point known as the origin, which represents the value 0 for each axis. Each axis acts as a number line extending in each direction from the origin out to infinity. The horizontal x axis extends to the right for positive values and to the left for negative values, while the vertical y axis goes upwards for positive values and downwards for negative values. A specific location in the plane is known as a point and is uniquely identified by an x and y value, usually written a (x, y) (more on those in a bit).

The plane is thus divided into nine regions: the origin, four quadrants, and four axis segments. Here are the characteristics of each region:

quadrant 1: x > 0, y > 0
quadrant 2: x < 0, y > 0
quadrant 3: x < 0, y < 0
quadrant 4: x > 0, y < 0
origin: x = 0, y = 0
positive x-axis: x > 0; y = 0
negative x-axis: x < 0; y = 0
positive y-axis: x = 0; y > 0
negative y-axis: x = 0; y < 0

Points

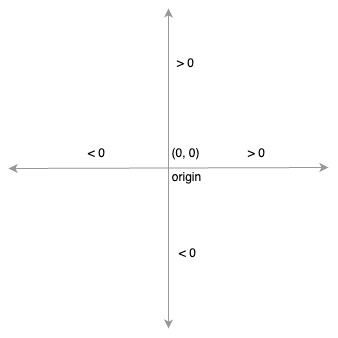
As mentioned above, a point is a unique location in the plane. It is said to be in that it has no height or width (and thus no length). A point is represented as a pair in the form (x, y) where x and y are the positions on the x and y axes respectively opposite the point:

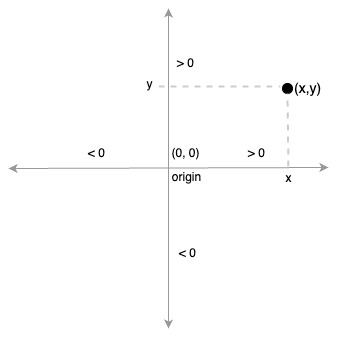
For the moment, we will restrict ourselves to integer-valued points (e.g., (0, 1) and (5, -7) as opposed to real points such as (3.1, -.2.45)).

Lines

Lines are represented by their two endpoints (strictly speaking, these are line segments — lines are infinite — but we'll use with this terminology for now).

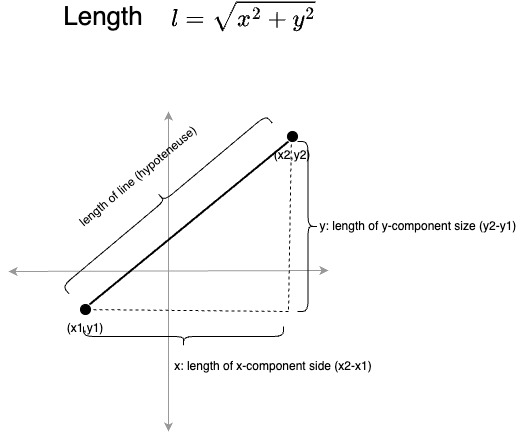
Length

A line has length or distance. Using the Pythagorean theorem, we see that the length between the two endpoints (the line itself, which is the hypotenuse of the right triangle) is the square root of the sum of the squares of the two sides (the x and y components).

Slope

A line has a notion of slope, which is the amount of change in y relative to a change in x. Slope is calculated by taking the ratio of the change in y between two points relative to the change in x for those same points:

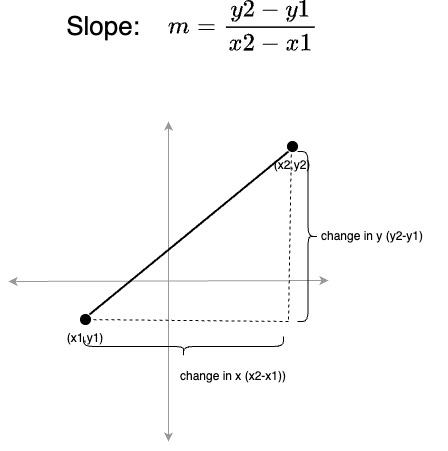
(Slope is usually represented by the letter m for various reasons).

Here are some properties of the slope of a line:

A slope of 0 means that y doesn't change, i.e., the line is horizontal (parallel to the x axis):
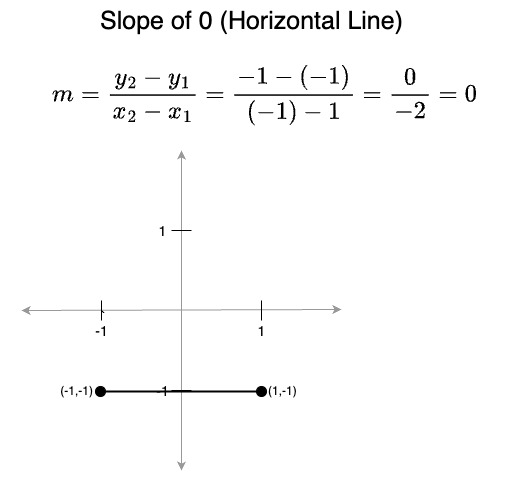
A slope greater than 0 represents a line the is moving upwards from left to right
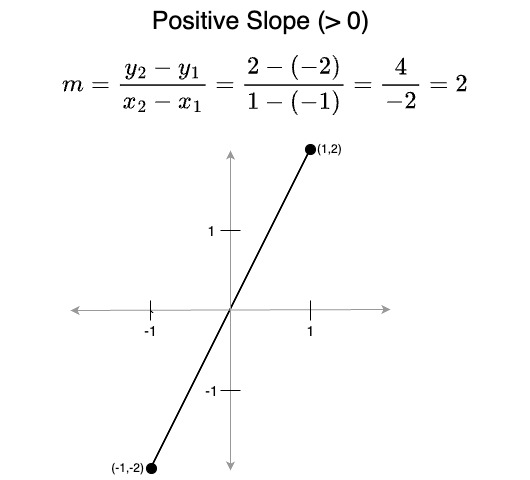
A slope less than 0 represents a line that is moving downwards from left to right
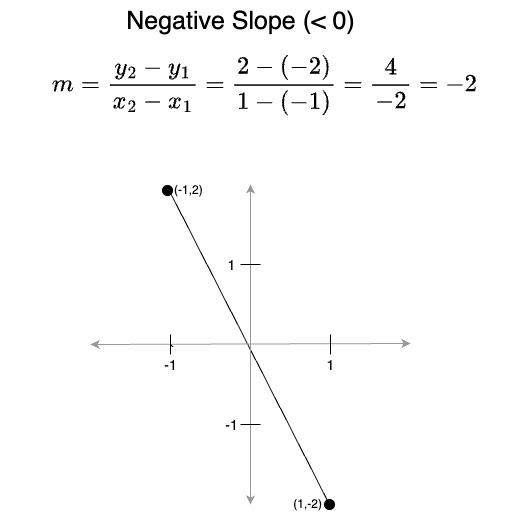
A slope of 1 means x and y change at the same rate; i.e., the line rises at a 45° angle (positive slope) from left-to-right
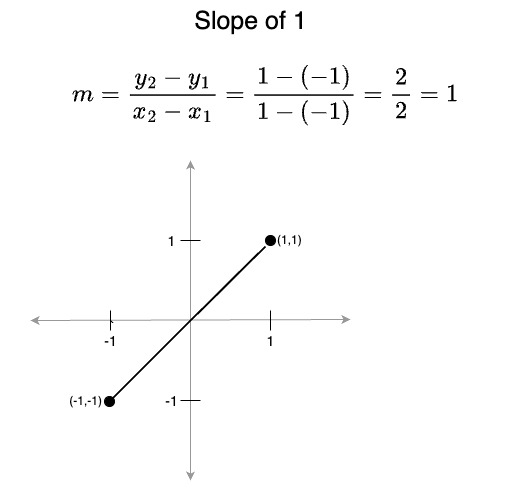
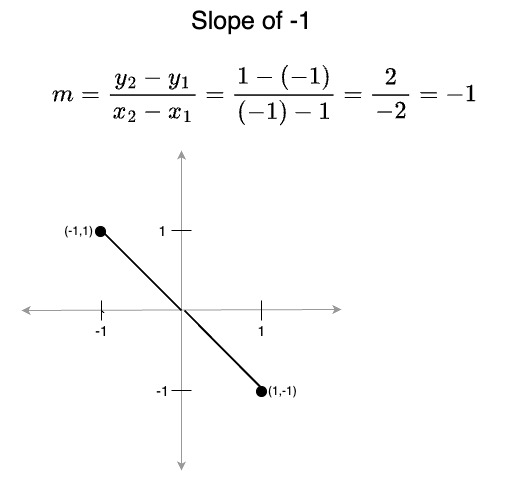
A slope of -1 means x and y change at the same rate, but here the line descends at a 45° angle (negative slope) from left-to-right
A vertical line has no slope - the x value is not moving, and thus the y component increases 'infinitely' with respect to x
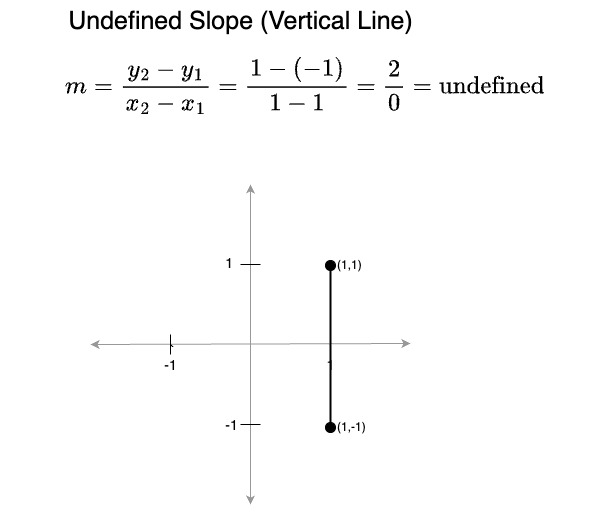
- In terms of the slope equation, the denominator is 0 (since both x values are the same) which would result in a division-by-zero, thus the slope is undefined
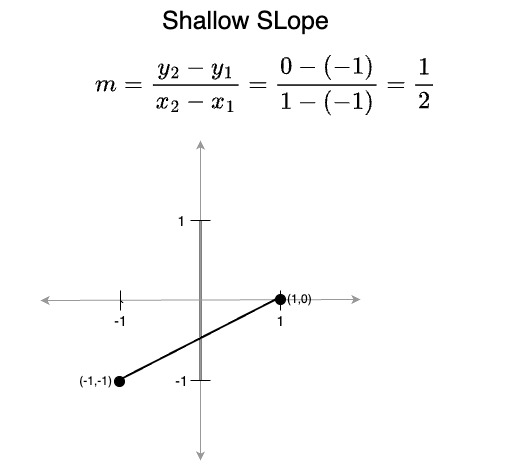
A slope between 0 and 1 (or between 0 and -1) is shallow, the line makes more horizontal progress than vertical progress
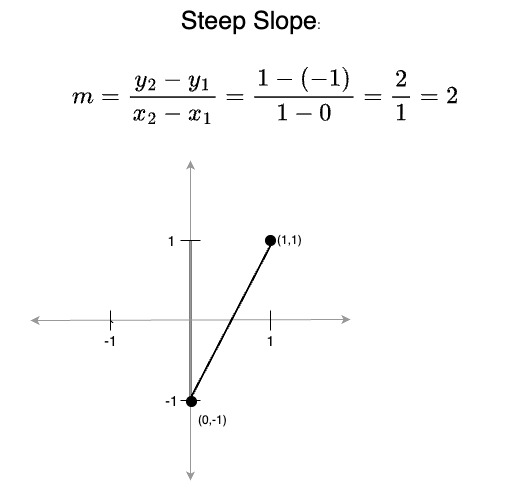
A slope greater than 1 (or less than -1) is steep, the line makes more vertical progress than horizontal progress

Line Pairs

The last item we will look at in the Cartesian plane will be pairs of lines. These are simply represented as two lines, each line represented — as above — using two endpoints; e.,g (0, 0), (1, 1) and (-1, -1), (-1, 0):

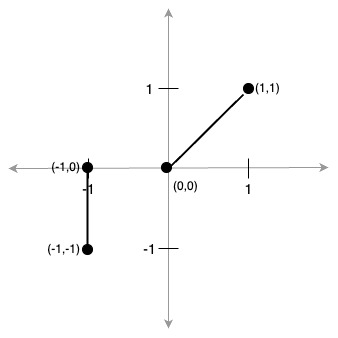
Parallel, and Perpendicular

Two lines are parallel if they have the same slope
- If they both rise at the same rate they will never intersect
On the other hand if the slopes of the two lines are negative reciprocals of each other (i.e., one has slope m and the other -1/m, then the lines are perpendicular to each other.

CISC 1115 Introduction to Modern Programming Techniques An Overview of Points, Lines, Line Pairs